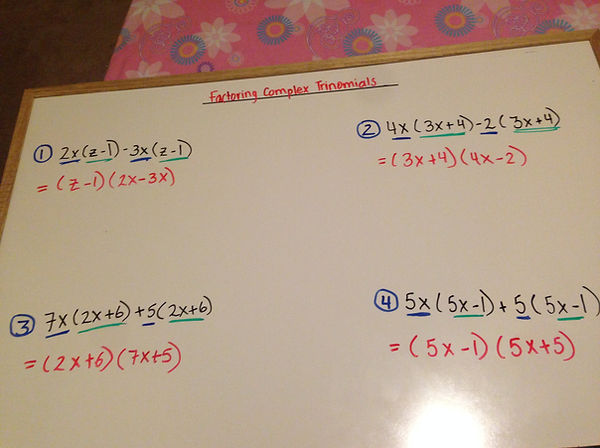Simple and Complex Trinomials

Many polynomials such as 5x2+2x+1 can be written as the product of two binomials of the form (x+r) and (x+s)

Keep in mind, when factoring a polynomial of the form ax2+bx+c(when a=1), we want to find the following..

1) Two numbers that ADD to give b *Also referred as product and sum*

2) Two numbers that MULTIPLY to give c

To help you understand this concept more clearly, use product and sum.

For example: x2+5x(Sum)+6(Product) _3_ x _2_ = 6

=(x+3)(x+2) _3_ + _2_ = 5

*Note if the product and sum do not equal to each other, its known as 'not possible'

For example: x2+2x+7

-Therefore, not possible

Now lets practice:

1) x2-29x+28 2) x2+6x+5

3) x2-52x+100 4) x2-10x+8

Answers:

Complex Trinomials have a coefficient besides than 1 in front of the x2 term

Before we can solve a Complex Trinomial, we have to learn the concept of the following;

1) Binomial common factoring

2) Factor by Grouping

Binomial common factoring:

Example 1: 3x(2x-3)-2(2x-3)

= (2x-3)(3x-2) < Basically here we collected the like terms which were(2x-3) and put brackets on the left over variables which were (3x-2)

Now lets practice:

1) 2x(z-1)+3x(z-1) 2) 4x(3x+4)-2(3x+4)

3) 7x(2x-6)+5(2x-6) 4) 5x(5x-1)+5(5x-1)

Answers:

Factoring by grouping:

Example 1: (ef+dg) (eg+df) [ There is no common factor amongest each brackets]

*However we can group the variables that have a common factor*

= (ef+df)(eg+dg) [Now we can common factor]

= f(e+d)+g(e+d)

[Now we use Binomial common factoring]

= (e+d)(f+g)

For solving a complex trinomial we can solve it with two methods:

1) Decomposition Method

2) Trial and Error

Decomposition Method: Trial and Error:

Now lets practice ( Preferred Decomposition)

1) 5x2-14x+8 2) 10y2-9x+2

3) 16x2+26x+12 [Always remember to common factor]

Quadratic RELATIONS